https://www.webpages.uidaho.edu/dl2/on_target/tv.htm

SIZING A PARACHUTE

==> Math modeling ==> Sizing a Parachute

by Levi Westra

Goal

Determine the size of a parachute needed to deliver a specified payload at a specified speed

Basic Concepts

When released from rest, a parachute will accelerate before reaching a steady speed.  This steady speed is called terminal velocity.  Terminal velocity is a consequence of equilibrium. That is, the sum of the forces on the parachute is equal to zero.  Forces acting on a parachute are shown in Fig. 1. 

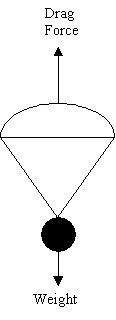
Figure 1

Weight (W) acts downward, through the center of mass.  The resistance of the ambient air creates a drag force D.  These forces are balanced once terminal velocity is reached.

W = D

Weight

Weight is given by W = mg, where m is the mass of the payload plus the mass of the parachute.  

Drag

Drag force is the retarding force acting upon a body as it moves through a fluid.  Engineers commonly predict drag using.

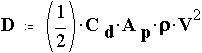
where Cd, the coefficient of drag, is found from experiments.  Values for a parachute are 0.8 < Cd < 1.2.  Note that Cd is unitless.  

The term Ap is the projected area of the object.  Imagine shining a light directly on an object.  The surface area of the shadow equals projected area.  Thus, for a hemisphere, the projected area equals the area of circle of radius r.   

Calculation of radius for a Parachute

To find the radius of a parachute, we equate weight with drag:

Using the drag formula gives

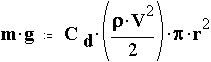
Solving for radius gives

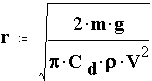
Example

Given an object of mass m = 100 g, find the radius of parachute needed to provide a terminal velocity of V = 7.5 m/sec.  Assume Cd = 1.2

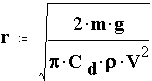
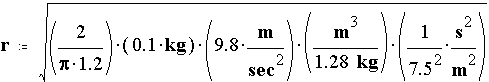
Note that this radius corresponds to the parachute as a three-dimensional object.  If one was to cut a round parachute out of a sheet of plastic, the radius of the plastic would need to be larger than this value. 

 

Sent from my iPhone